Räkna ut accelerationskurvor

Hej!

Nu är jag trött på att tycka att det är pinsamt att fråga

Jag håller på att bygga ett excel-ark med lite beräkningar på min bil, en Impreza. Har vridmomentskurva, utväxlingar, hjulmått, luftmotstånd mm och tänkte få ut lite trevliga diagram.

Jag är inget matte- eller fysikgeni överhuvudtaget, men har lite koll på krafter, arbete, effekt osv. Nu är frågan, hur tusan räknar jag ut acceleration på ett korrekt sätt? Då det är effekten som bestämmer acc så funkar ju inte a = F/m?

Detta har diskuterats tusen gånger förr, jag vet... Men jag hittar inget exempel på hur man räknar på det. Eller jo, förresten, men http://cvt.com.sapo.pt/performances/performances.htm verkar lite förenklad, eller?

Jag har försökt räkna lite. Stämmer hyfsat men hur bra det i ett bredare persktiv har jag ingen anning om.
se
https://rejsa.nu/forum/viewtopic.php?t=3143&highlight=hj%E4rnjumpa . . . .

Vad jag saknar tider, effekter utväxlingar,vikter, masströghetsmoment mm får fler bilar för att verifiera att beräkningsmodelen funkar eller ej.

Har försökt hänga med i dina beräkningar, men tappat bort mig då Fx först sägs vara den sammanlagda kraften som måste övervinnas för att accelerera bilen, men sedan blir effekten(?)

Kan du göra ett exempel med riktiga siffror? Ta gärna bort tröghet och verkningsgrad, dvs väldigt enkelt Vore himla uppskattat

Hmm skall göra ett försök. Obs "ett" är pluralis

Fx=P*vg/c
Var det där det sket sig?????
Jo, kraft gånger hastighet är effekt, allså Fx * c = P * vg (vg är ju sortlös)

Ajaj, min stackars hjärna

Fx = P*vg/c visar alltså vilken effekt (P) som behövs för att bibehålla hastigheten, nä? Känns som att jag tänker från fel håll...

Det jag vill ha är ett diagram över hur hastigheten ändras över tid.

Annan fråga... Om man tittar på en g-mätare i en bil som accar, följer då mätaren vridkurvan eller effektkurvan?

Snart kommer ett genom- eller sammanbrott

Nu har jag inte tittat på Johans beräkningar, men allmänt är det så att en motor vid ett visst varvtal har, eller kan ha snarare, en viss maximal effekt. Denna effekt ger en kraft vid hjulen som beror på hastigheten (F=P/v). Det försvinner förstås även lite i förluster under vägen till hjulen. Om denna kraft är annorlunda än bilens motstånd(skraft), FD, så får man en acceleration. Positiv om kraften är större och negativ om den är mindre. Kraftöverskottet, dF=F-FD, ger alltså accelerationen a=dF/m, där m är bilens massa. Om man bortser ifrån masströghetsmomentet i de roterande delarna.

Men då låter det som att vi är tillbaka till a=F/m, vilket borde betyda att accet är bäst på vridtoppen, vilket det inte är. Det är ju vridmomentet som ger kraften direkt, multiplicerad med utväxlingen. Om man räknar så behöver man aldrig ta med effekten.

strat skrev:

Men då låter det som att vi är tillbaka till a=F/m, vilket borde betyda att accet är bäst på vridtoppen, vilket det inte är. Det är ju vridmomentet som ger kraften direkt, multiplicerad med utväxlingen. Om man räknar så behöver man aldrig ta med effekten.

Att accet inte är bäst vid vridtoppen i tex 5:an förstår jag, då luftmotståndet är en bit högre än, säg, 500-1000 rpm före vridtoppen. Beroende såklart på vid vilket varvtal, dvs hastighet vridtoppen inträffar.

Men i t.ex. 2:an, innan luftmotståndet hunnit bli särskilt stort, borde väl bilen acc:a som bäst vid vridtoppen?

Njae. Om man betänker att effekt är en definition av hur mycket arbete (kraft i rörelsens riktning en viss sträcka) som utförs under en viss tid så blir det snurrigt, i alla fall för mig Mer effekt - mer jobb gjort snabbare.

strat skrev:

Men då låter det som att vi är tillbaka till a=F/m, vilket borde betyda att accet är bäst på vridtoppen, vilket det inte är. Det är ju vridmomentet som ger kraften direkt, multiplicerad med utväxlingen. Om man räknar så behöver man aldrig ta med effekten.

Nej, varför det?
F och därmed dF är störst när P är störst, vid varje given hastighet. Att man kan räkna ut kraften m.h.a. vridmomentet betyder inte att kraften vid däcket är störst när vridmomentet ifrån vevaxeln är störst. Vridmomentet är bara en konsekvens av effekten och utväxlingen, inte tvärtom. Det är ju bara att sätta en planetväxel på vevaxeln så kan du ändra vridmomentet ut ur motorn, men effekten är fortfarande densamma.

Att förflytta bilen initialt kräver ingen effekt alls, utan bara kraft. Effekten ifrån motorn måste då "försvinna", vilket den gör i kopplingen och ev. däckspinn, alltså ökning av värmeenergin.

strat:
Titta lite längre ner i min uträkning så står det
a=(Fx-FL-Fr)/(m+mj) allså en kraft delat med en massa.
Där Fx är den kraft som kommer från motorn.
Här i den axeleration som finns att tillgå när rull och luftmotståndet är borttaget.
mj=masströghetsmomentet omgjort till en vikt som läggs på bilens statiska vikt. (m+mj)

Så hur man än vänder sig så sitter arslet bak

Hmm, det kanske blev lite abstrakt det där. Ett försök till praktisk illustration:

Det som är konstant är hastigheten och därmed hjulets rotationshastighet.
Säg att vridmomentet är helt konstant vid alla varvtal och hjulets rotationshastighet av någon konstig anledning är 3000 rpm. Vid 3000 rpm i motorn har man då en utväxling på 1:1 och vridmomentet ute vid hjulet är detsamma som i motorn. Om man ökar motorns varvtal till 6 000 rpm måste man ändra utväxlingen till hälften(eller heter det dubbla kanske?) för att hålla samma varvtal på hjulet och därmed får man även ett dubblat vridmoment ute vid hjulet, alltså dubblad kraft. Även om motorns vridmoment hade minskat med 25% vid 6000 rpm, så hade vridmomentet vid hjulet fortfarande varit högre än då motorn varvade 3000 rpm.

Nu tar vi det här från början.

F=m*a

Vad är a????
Jo axeleration
Vad är axeleration???
Jo hastighetsökning per tidsenhet.
Hur tänkas rätlinjig ax???
a=(c2-c1)/t

Överens?????

Jarå, överens

Kanske bättre att jag förklarar hur jag räknat.

- Jag har motorns vridmomentskurva.

- Jag multiplicerar den kurvan med den totala utväxlingen, inkl. hjul, och får så en kraftkurva för varje växel.

- Räknar också ut en motståndskurva (luft och rull).

- Drar bort motståndet från hjulkraften och delar med massan.

Nu har jag kurvor över hur hög accelerationen är över hela registret och på alla växlar. Kurvorna liknar ju i stort sett vridmomentskurvan (doh) och har således bäst acc på vridtoppen.

Excel filen finns på: http://www.claeswikdahl.com/files/imprezapower.xls

Gör jag nåt fel så här långt?

Ser helt ok ut.

om du plottar tillgänglig kraft för acceleration (x-axel) mot hastighet (y-axel) för alla växlar i ett och samma diagram kan du också se vid vilka varvtal du ska växla för maximal acceleration.

EDIT: Eftersom du redan har accelerationskurvor är det ju enklare att använda dem i det här fallet än att använda kraftkurvor...

strat:
Hängde du med på mitt resonemang om varför det är effekttoppen som ger den maximala accelerationen?

om du som André sa plottar accelerationen som funktion av hastigheten så syns det lite bättre.

Ett exempel kan t.ex. vara om du kör på 5:an vid max vridmoment, alltså 4 000 rpm. Då går det i 160 km/h och du har en kraft på 2 689 N. Om du kör på 4:an i samma hastighet varvar det knappt 5300 rpm och du har då en kraft på ca 3 200 N, vilket alltså är högre trots att du inte ligger på optimalt vridmoment.

Du har gjort så här:
Mv*u/r=m*a+c^2*0,5*cw*A*rå+m*g*kr

Mv*u/r är vad jag kallar Fx
m*a är vad jag kallar Fa med den skilnad att jag har (m+mj)
c^2*0,5*cw*A*rå är vad jag kallar Fl
m*g*kr är vad jag kallar Fr

-----------------------------------------------------------
om vi nu tittar på Mv*u/r och P/c

P=Mv*w
w=n*pi/30
P=Mv *n*pi/30
c=n/60*D*pi/u --> n=c*60*u/D/pi

P=Mv*c*60*u/D/pi*pi/30 ---> P=Mv*c*u*2/D
P=F*c ---> F=P/c
F=(Mv*c*u*2/D)/c ---> F=Mv*u*2/D
Där r=D/2
F=Mv*u/r

Allså Mv*u/r = P/c
Är du med???????
Kolla eller tro mig det är samma sak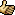
Effekt eller moment spelar ingen roll.
##########################################
Vad du inte tagit hänsyn till är masströghetsmomentet på typ svänghjul, drivpaket, bromsskivor, hjul mm, allså allt som rotera.

Tumme pekfinger så är mj ca 400-500kg på 1an, hua japp det är mycket.
Detta beroende på att masströghets(Jm) momnetet som skall flyttas från motor till drivaxeln är utväxlingen i kvadrat
Allså J*u^2 (där u typ 1an 12-15:1)

Deffenitionen för masströghetsmomet är vikt gånger radie i kvadrat därav
blir mj=J/r^2

mj=Jm*u^2/r^2 (detta är bara då motorns masströghetsmomnet, svänghjul, vevaxel, remskivor mm)
############################################

Huuua Du är på rätt spår tror jag

En liten text jag stulit från STCS som jag tycker är bra som berör ämnet.
citat:
Antag att du ska köra skit i en skottkärra. Vridmomentet är hur mkt du orkar ha på kärran för att bära upp den. Varvtalet är hur fort du går/springer med kärran.

om du nu får i uppgift att flytta en skithög från en plats till en annan så kan vi säga att effekten är ett mått på hur snabbt du blir klar med uppgiften. En liten ettrig motor med lågt vridmoment får varva mkt för att utföra samma arbete/effekt medan en stor lågvarvig motor lassar på rejält i varje kärra, men masar sig fram långsamt så de blir klar samtidigt. De har alltså samma effekt.

Vridmomentet är ju hur kraftigt kolvarna trycks ned vid förbränningen och vrider runt vevaxeln. Effekten är summering av mängden kraft i varje kolvslag ggr hur många sådana det görs under en viss tid.

Effekt är ju ett mått på ett arbete eller en viss energimängd. I exemplet ovan blir enheten för effekt: Mängd skit förflyttad per sekund! Det går åt en viss mängd arbete per sekund för att accelerera en bil upp till en viss hastighet.

Det enda chefen bryr sig om är ju hur snabbt man flyttar skiten, och inte hur man går till väga. Slutsatsen är att det är effekten som (avgör/är ett mått på) hur snabbt en bil accelererar. Vrid och varv beskriver bara hur effekten uppnåtts skulle man kunna säga.

Här har jag gjort en översättning av en artikel skriven av Mark ortiz.
Consulterad i dessa frågor av Race car Engeneering. Vi kan fastslå att
högre acceleration kräver mer effekt levererad från motorn. Ju mer effekt motorn levererar, ju bättre acceleration.
Ursäkta om översättningen är lite hastigt gjord.

CIT,
Den gamla frågan om vridmoment / HKR.

Mer hkr gör bilen snabbare. Rätt eller fel?

Frågeställningen togs upp i en tidning, skriven av en ansedd författare i ämnet. Till min förvåning konstaterade han att antagandet var felaktigt!
Han förklarade att om alla omständigheter var desamma, ikl däcksstorlek, så kräver mer acceleration mer vridmoment. Inte nödvändigtvis mer HKR.

Vad det här resonemanget missar är att eftersom effekt är en produkt av varvtal och vridmoment, så blir mer vridmoment vid drivaxeln med automatik mer hkr.

om vi har mer vridmoment vid ett givet axelvarvtal, vad kan vi då säga om situationen vit svänghjulet? Har vi mer vridmoment här? Inte nödvändigtvis. Författaren själv menar att vi kan ha ett identiskt vridmoment, och större vridmomentsökning beroende på lägre utväxling.

Så, om det är samma vridmoment vid svänghjulet, identiskt varvtal vid drivaxlarna, samt kortare utväxling, vad vet vi då om motorns varvtal?
Jo, det har ett högre varvtal i direkt proportion till utväxlingen.
Samma sak igen, effekten är en produkt av vridmoment och varvtal.
Därför, om vridmomentet är detsamma och varvtalet högre, HKR är även större vid svänghjulet.

om drivaxeln har ett större vridmoment vid en given hastighet, säger ingenting om vridmomentet vid svänghjulet. Men vi kan med säkerhet säga att både produkten av motormoment och utväxling, och produkten av motormoment och varvtal, är större.

Sett på ett annat sätt, effekt är ett värde på energiflöde. För att få motorn att lägga till kinetisk energi till bilen i en högre grad, så måste energi flöda i högre grad från motorn.

Notera att detta är ennågot annorlunda fråga än att bygga en "hästkraftmotor" eller en "vridmomentdmotor". Vad som räknas vid ett speciellt tillfälle är hkr, VID DETTA TILLFÄLLE, inte vid toppen av effektkurvan. I många situationer, speciellt i korta ovaler utan växling, så går bilarna ur kurvorna på ett varvtal närmare vridmomentstoppen än effekttoppen. Under sådana omständigheter är det bra att bygga en motor iriktad på vridmomentstopp för bättre varvtider. Men, vi talar fortfarande om HKR ökningar, som kommer från mer vridmoment vid samma varvtal. Eller, alternativt genom samma vridmoment men mer varvtal och utväxling.

Så, ett bredare effektband är värdefullt,ock kan vara mer värt än hög peak effekt. Men, vid ett givet tillfälle, en given hastighet, så betyder ett högre vridmoment vid hjulaxeln en högre motoraxeleffekt. Men ger ingenting vid handen om motorns vridmoment.
Slut CIT.
MVH
Göran Malmberg.

En annan "lustighet" i ämnet:
I en vanlig kolvmotor så är det effekten som är konstant oberoende av bilens hastighet, eftersom man inte kan öka varvtalet hur mycket som helst. Även om den skulle råka hålla så funkar det inte gasdynamiskt med förbränningen - den hinner inte med.

För jetmotorer är det istället kraften som är konstant med hastigheten och effekten som alltså ökar med hastigheten. Kan bli ganska häftiga effekter med en motor som har en dragkraft på 100 kN i 500 m/s (50 000 kW). Typ 5 000 villapannor - villapannsbeståndet i en mellanstor svensk stad.

Jahaja, så allt stämmer? Keppen i hjulet för mig var nog att jag trodde att jag skulle få acckurvor som såg ut som effektkurvan istället för vridkurvan. Men det är alltså så, om man tittar på en växel bara, att varvräknarnålen går som snabbast över vridtoppen, i mitt exempel 4000 varv?

Citat:

Sett på ett annat sätt, effekt är ett värde på energiflöde. För att få motorn att lägga till kinetisk energi till bilen i en högre grad, så måste energi flöda i högre grad från motorn.

Det är just detta som förbryllar mig. I mitt exempel så tillför ju motorn mer energi vid toppvarv än vid toppvrid. Ändå accar den långsammare. Effekten vid hjulet är väl alltid densamma, oavsett utväxling?

Men för att få bäst acc genom växlarna är det ju helt logiskt att man bör dra bilen så långt det går på den lägre växeln, så länge man inte får en större kraft vid hjulet på den högre.

Tack för alla svar förresten. Det här är något som gnager mig hyfsat ordentligt