| Allt Nytt | Kalender | Racerbanor | Arrangörer | Forum | Varvtider/Loggar |


 |
Allmänt banåkaforum
 Lättning till absurdum eller viktväktare A la racing.
Lättning till absurdum eller viktväktare A la racing.
|
6886 besök totalt |
|
Re: Lättning till absurdum eller viktväktare A la racing.
Men om man har råd så......  [/quote] [/quote]
Men du Nisse, blir det verkligen lättare för att man klär ratten med kolfiber? 
Johan Sherwood Racing |
||||||
_________________ "Full fart; spar tid." /Igino Cazzola Blandar italienskt, tyskt och engelskt i en härlig gröt. |
||||||
Då blir det lättare, det var Tomas jag snacka med, men vart nog lite förvirring 
|
||||||
Menar inte Daniel att bilens rotationscentrum vid kurvtagning utan slip är vid bakaxeln och att man därför bör placera så mycket massa som möjligt där? Hmm, få se nu. Masströghetsmomentet, Izz = rumsintegral (x^2 + y^2)dm. Kan den verkligen bli mindre någon annanstans än i masscentrum? Får väl tänka ut det, om jag orkar. Men å andra sidan blir den förstås mindre om man placerar massan vid masscentrum och masscentrum hamnar närmare bakaxeln om man placerar massan så långt bak som möjligt. Frågan är vad som har störst betydelse? _________________ /Anders Ytterström #24, #64, #88 |
||||||
|
Då skall vi se här(synd att jag har mina mekanikböcker på jobbet...):
Rotationsaxel genom masscentrum, c.g. (S=rumsintegraltecken): Izz = S(x^2+y^2)dm En annan rotationsaxel, på avståndet x1 och y1 ifrån c.g.-axeln: Izz2 = S(x2^2 + y2^2)dm = {x2 = x-x1, y2=y-y1)} S((x-x1)^2 + (y-y1)^2)dm = S(x^2 - 2xx1 + x1^2 + y^2 - 2yy1 + y1^2)dm = S(x^2 + y^2)dm + S(x1^2 + y1^2)dm - S(2xx1)dm - S(2yy1)dm x1 och y1 är ju konstanta och kan flyttas ur alla integraler: S(x1^2 + y1^2)dm = R^2Sdm = m(R^2) S(2xx1)dm = 2x1S(x)dm S(2yy1)dm = 2y1S(y)dm S(x)dm = S(y)dm = 0, enligt definitionen av c.g.. S(x^2 + y^2)dm = Izz Så då blir det Izz2 = Izz + m(R^2) Alltså fås minsta Izz2 för axeln som går igenom c.g., eftersom R=0 där. 
Det betyder alltså att för ett givet Izz i c.g. så skall man rotera så nära den axeln som möjligt och därför är det bra att flytta vikten så långt bak i skuffen som möjligt och få minimalt R, men samtidigt minskar man Izz om man lägger den extra massan nära c.g.. Jaha, nytt optimeringsproblem... 
_________________ /Anders Ytterström #24, #64, #88 |
||||||
|
Efter en vilopaus tar jag väl det här också då:
Vi har 4 pkter: 0 - gamla c.g. för massan, M, innan den lilla massan m las till. cg: Den nya c.g. för den nya massan (M+m) som ligger på avst. r1 ifrån 0. b: Rotationscentrum, vid bakaxeln om ingen slip. Ligger r2 ifrån 0. 3: Placeringspunkten för exramassan, m. Ligger r3 ifrån 0. Izz är det gamla Izz innan m tillsattes, det nya Izz för punkten 0 när m läggs dit blir då: Izzny = Izz + mr3^2 Momentjämvikt kring cg ger: r1M = (r3-r1)m => r1 = r3m/(M+m) Då blir masströghetsmomentet i cg: Izzcg = Izzny - (M+m)r1^2 = Izz + mr3^2 - r3^2m^2/(M+m) Masströghetsmomentet i b: Izzb = Izzcg + (M+m)(r2-r1)^2 = Izz + mr3^2 - r3^2m^2/(M+m) + (M+m)(r2-r1)^2 = Izz + mr3^2 - r3^2m^2/(M+m) + (M+m)(r2^2 - 2r1r2 + r1^2) = Izz + mr3^2 - r3^2m^2/(M+m) + (M+m)r2^2 - 2r2r3m + r3^2m^2/(M+m) = Izz + mr3^2 + (M+m)r2^2 - 2r2r3m Derivera Izzb med avseende på r3: Izzb-prim = 2mr3 - 2mr2 Sätt lika med 0 för att hitta optimum: 2mr3 - 2mr2 = 0 => r3 = r2 för att Izzb och därmed rotationströgheten skall bli så liten som möjligt Vikten skall alltså placeras i rotationscentrum precis som Daniel sa, vilket på sätt och vis kan tyckas elementärt, men nu är det även bevisat.  
_________________ /Anders Ytterström #24, #64, #88 |
||||||
Haha 
|
||||||
 Rotationscentrumet ligger väl kurvradien innanför bilen? Rotationscentrumet ligger väl kurvradien innanför bilen?
_________________ "Full fart; spar tid." /Igino Cazzola Blandar italienskt, tyskt och engelskt i en härlig gröt. |
||||||
|
Det var bara ett antagande att rotationscentrum låg vid bakaxeln, eller Daniels approximativa antagande, rättare sagt. Men för beräkningen spelar det ingen roll var det ligger, den kan lika gärna ligga på månen. Det är alltså bilens rotationscentrum när man ändrar kurvradie som gäller och inte kurvradiens rotationscentrum. På rakan är ju kurvradiien oändlig för att i kurvan övergå till kurvradien och för att få till den ändringen behövs en acceleration, där Izz kommer in. I själva kurvan är ju inte Izz intressant för då är just den aktuella accelerationen noll, om man kör med jämn kurvradie.
_________________ /Anders Ytterström #24, #64, #88 |
||||||
Påminner om några citat här i spalten. "Bara för att uträkningen är rätt behöver inte antagandet var det". 
Göran Malmberg. _________________ Hemipanter Göran Malmberg 
|
||||||
Mitt antagande var inte bara approximativt utan korrekt, om vi bortser från slipvinklar. Bilens rörelse i en kurva kan då beskrivas av translation längs x och rotation kring z. Detta ger kurvradien. Sen var det bra att Anders visade på tröghetsmomentets betydelse avseende att det växer med r^2 för en infinitesimal massa på avståndet r. Vi får inte glömma att tröghetsmomentet utgörs av varje litet masselement på avståndet r^2 från den koordinataxel vi väljer för betraktelsen. Alltså kan vi inte använda totalmassan och avstånd till masscentrum. Utan vi måste integrera för varje infinitesimalt masselement på bilen. mvh Daniel _________________ Daniel Nihlén Porsche 964 C2  såld... såld...
PCS 8040 "Porsche motoring is and always will be driving in its purest form." Ferry Porsche |
||||||
Ehh, om vi tar det här på gymnasienivå istället så tycker jag det här känns som Steiners sats, är det korrekt uppfattat? _________________ Pär Hylander |
||||||
|
Daniel,
Det var inget påstående från min sida att antagandet skulle varit fel. Utan att Anders kommentar om att det för hans uträkning inte spelade någon roll om det var korrekt. Då damp själva citatet ner i huvet på mig, å jag tyckte det lät kul. Sensmoralen är att så kan vara fallet ibland, å saker gjorda i kolfiber kan även vara bra. Göran Malmberg _________________ Hemipanter Göran Malmberg 
|
||||||
|
|
||||||
jo, men det är väl just det som är det approximativa. För övrigt har ju Göran rätt i att om man stoppar in skit så kommer det ut skit, även om allt därimellan är korrekt uträknat. _________________ /Anders Ytterström #24, #64, #88 |
||||||
Hehehe! Shit in shit out vet ju både du och jag är en sanning i beräkningsvärlden. Jo, det här med slipvinklarna gör ju det totalt ointressant att sätta en fix axel mitt ibakaxeln för att använda som något statiskt tröghetscentrum. Vi måste ju egentligen räkna från andra hållet och börja med krafterna som verkar på respektive axel, sicaccelerationskonstanten för respektive axel och slipvinklarna för respektive axel. mvh Daniel _________________ Daniel Nihlén Porsche 964 C2  såld... såld...
PCS 8040 "Porsche motoring is and always will be driving in its purest form." Ferry Porsche |
||||||
|
Här har jag en förhoppningsvis bätter redogörelse rörande Cg. Som synes är balansen i bilen avhängig av hur bilens massa vill vrida sig runt Cg. Massan bör därför koncetreas dit för en lättvridbar bil. Cg är det centrum varifrån massan påverkar bilen, och därmed hur hjulen belastas via fjädringssystemet.
Det finns andra rörelsecentrum på bilen som betingas av mekaniska orsaker. Men det är bilens massa centrum som via hävarmen från Cg påverkar vad som händer med bilen.. 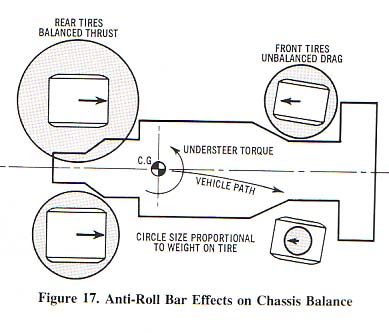

_________________ Hemipanter Göran Malmberg 
|
||||||
|
Göran:
Bra illustration, det är ju klart lättare att hålla sig till vad som händer runt masscentrum eftersom vi vet var det är. Det jag försökte stressa innan var att om vi betraktar bilens rörelse som rotationen kring masscentrum så består den även av en translation av masscentrum i någon riktning också (förutom i x-led för ett fordonsfast koordinatssytem), såvida inte som jag exemplifierade tidigare med att slipvinkeln bak = (styrutslag fram - slip fram) och viktfördlening 50-50 så att rotationen verkligen hamnar i masscentrum. Detta handlar ju bara om var vi väljer att placera vårt lokala koordinatsystem i bilen, masscentrum är ju att föredra. Det är om vi slår ihop vektorn för translation av masscentrum och den för rotation kring masscentrum som vi får en rotation kring en annan punkt än just masscentrum. Denna punkt flyttar på sig beroende på hur slipvinklarna ser ut och är inte statisk som masscentrum kan anses vara. Men för enkelhetens skull när vi räknar så håller vi oss till masscentrum, men om vi säkert vet att den rena rotationen verkligen sker i närheten av en viss punkt kan vi sänka masströghetsmomentet kring vridaxeln genom att placera "onödig" massa där om det finns något att tjäna på det. Allmänt: Det roliga när vi diskuterar är att jag har en massa teoretisk kunskap som jag aldrig i praktiken applicerat och tänker i en massa hypotetiska fall som är relativt ointressanta för det verkliga fallet. Du har ju applicerat din teori och det gäller ju även Butterfly m.fl som gillar de här diskutionerna. Jag försöker bara kasta lite ved på brasan genom att vända och vrida på det vedertagna och se det ur en rent teoretiskt mekaniksynvinkel. Daniel _________________ Daniel Nihlén Porsche 964 C2  såld... såld...
PCS 8040 "Porsche motoring is and always will be driving in its purest form." Ferry Porsche |
||||||
|
Daniel,
Toppen. Vi måste självfallet diskutera utifrån ämnet. Jag är alltid livrädd för att vad jag säger ska uppfattas som kritik. Ifrågasättnde är bra. Det visar om en teori håller sträck. "så består den även av en translation av masscentrum i någon riktning också (förutom i x-led för ett fordonsfast koordinatssytem)" Jovisst, om bilen kränger så förflyttas massa centrum med tan på krägningsradien. För att ta ett exempel. I mitt fall blir det vid 1g, massaförflyttning=2 tan*300. 10,47mm. På en spårvidd av 1600mm gör det 1350kg*10,47/1600=7,99Kg mer tyngd på ena sidans hjulpar. Att lägga till det som orsakas av viktförflyttningen pga hastigheten i kurvan. "viktfördlening 50-50 så att rotationen verkligen hamnar i masscentrum" om slippvinkeln skapar ett annat rotationscetrum än mitt i Cg (tar bort H-öjdledes här) så blir bilen över eller understyrd. Graden av ö-u nderstyrning är just aståndet mellan axlarna. Ganska tjusigt va? "Det är om vi slår ihop vektorn för translation av masscentrum och den för rotation kring masscentrum som vi får en rotation kring en annan punkt än just masscentrum. Denna punkt flyttar på sig beroende på hur slipvinklarna ser ut och är inte statisk som masscentrum kan anses vara." En lätt omskrivning. "Men för enkelhetens skull när vi räknar så håller vi oss till masscentrum, men om vi säkert vet att den rena rotationen verkligen sker i närheten av en viss punkt kan vi sänka masströghetsmomentet kring vridaxeln genom att placera "onödig" massa där om det finns något att tjäna på det". Vi får två parametrar att ta hänsyn till här. Antingen större tröghet runt CGH, eller förflyttad CGH=viktfördelning fram-bak. Man får välja det som tjänar syftet bäst. Man kan också antingen flytta Cg till "slippcentrum" eller slippcentrum till Cg via t,ex krägningsfjädrarna. Men VILL vi ha en understyrd bil så är vi betjänta av "två centrum". "Allmänt: Det roliga när vi diskuterar är att jag har en massa teoretisk kunskap som jag aldrig i praktiken applicerat och tänker i en massa hypotetiska fall som är relativt ointressanta för det verkliga fallet. Du har ju applicerat din teori och det gäller ju även Butterfly m.fl som gillar de här diskutionerna. Jag försöker bara kasta lite ved på brasan genom att vända och vrida på det vedertagna och se det ur en rent teoretiskt mekaniksynvinkel." Jag vill inte säga att någon teori är min direkt. Vi kan säga att tolkningarna är mina. I övrigt så kommer allt från mina diskussioner med experter samt racing böcker. Å det tar några år att nöta in att det man läst å hört stämmer med praktiska ändringar på bilen. Det gäller att "bokföra" varenda förändring för att kunna få ihop ett sammanhang. Göran Malmberg. 
_________________ Hemipanter Göran Malmberg 
|
||||||
Först så  sen så sen så  NU NU 
"Still confused but on a higher level" _________________ Johan Lundberg *BBDB* Ex Marcos 2T EX Marcos 1600 GT Nu Lotus Elise S1 KR1 |
||||||
 |
Allmänt banåkaforum
 Lättning till absurdum eller viktväktare A la racing.
Lättning till absurdum eller viktväktare A la racing.
|
6886 besök totalt |
